NOTES
Navier-Stokes Existence and Smoothness Problem
Let me say up front, I have not solved this problem, nor am I in the running. I came to math late in 2016 after a lifetime of music study, and while I am building a solid trellis upon which to grow my imagination, it will take me many years to capitalize on my potential. That being said, the Millenium Prizes are my one of my favorite sporting events, and the Navier-Stokes Existence and Smoothness Problem is my home team I’m rooting for to emerge next.
Overview
Taken with the Euler equations, Navier-Stokes describes the motion of a fluid in $R^{n}$ where $n$ = 2 or 3. We solve the equations for an unknown velocity vector $u(x, t) \in R^n$ and pressure p(x, t) \in R^n**, defined for some position $x\in R^n$ and $t \geq 0$.
Terms
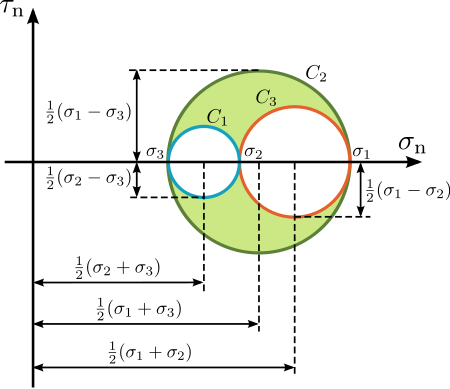
- Mohr’s Circle: 2D graphic of the transformation law of the Cauchy stress tensor.
- Galillean relativity: The laws of motion are the same in all inertial frames.
- Cauchy stress tensor: Represented as a matrix of nine datapoints completely defining the state of stress at a point in a material.
- isotropic: Uniformity in all directions.
- Newton’s Second Law (re: a particle): (mass)(acceleration) = sum of forces $$m\vec{a} = \sigma\vec{F}$$ $$m/V\frac{d\vec{v}}{dt} = \sigma\vec{F}/V$$
- Continuum Hypothesis (CH): “There is no set whose cardinality is strictly between that of the integers and the real numbers” (proposed by Georg Cantor in 1878, and proved by Paul Cohen in 1963, building on Godel’s 1940 work).
The Equations
Stokes stress constitutive equation: $\tau = 2\mu\epsilon$ with $\epsilon=0.5(\nabla u + \nabla u^T)$
References
- Existence and Smoothness of the Navier-Stokes Equation, by Charles Fefferman
- Wikipedia